Rotating Array
There is a classica cryptography algorith named Caesar Cipher. In this algorithm we will be having all the 26 characters (in array arr) and we rotate the array some number of times (say 2 times and is stored in n).
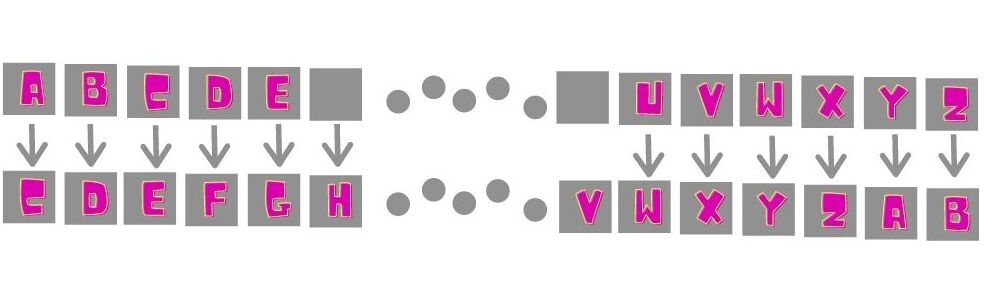
So once we rotate the array two times, we will be having new array like below.
- A -> C
- B -> D
- C -> E
-
D -> F …
- X -> Z
- Y -> A
- Z -> B
To achieve this programatically below program will be helpful. We have two algorithms for this.
Divide Reverse, Reverse, Reverse
Divide In this algorithm we will be virtually splitting the array into two parts. First part will be from start position (0) to number of times we want to rotate. Second part is from next character of rotation times to end of array.
private void rotateUsingReverse(int[] arr, int rotationTimes){
// In one access two elements are swapped
reverse(arr, 0, rotationTimes-1);
reverse(arr, rotationTimes,arr.length-1);
// here we will have another half number of access.
reverse(arr, 0,arr.length-1);
}
// In one access two elements are swapped
private void reverse(int[] arr, int startIndex, int endIndex){
while (startIndex<endIndex){
int tempNumber = arr[startIndex];
arr[startIndex] = arr[endIndex];
arr[endIndex] = tempNumber;
++startIndex;
--endIndex;
}
}
Reverse, Reverse, Reverse
So We have virtually split the array into two segments. Now we take the first segment which ll have number of times the rotation to be made (say if the rotation is 5 times we will have 5 elements).
We will be reversing this first small array, by the following step.
- First we will be keeping a temporary copy of initial index(0) in temp variable.
- We will now copy the last element (value at endIndex or value at index 4 for 5 elements), to initial Index
- Next we will copy the value at inital index to the endIndex
- Next we will increment the startIndex by 1
- Next we will decrease the endIndex by 1.
We will be continuing the above step till startIndex is less than endIndex.
Similarly we will do for the next segement of array. Now we will be reversing the whole array. Below example will help you understanding.
int[] arrayOfNumber = {1,2,3,4,5,6,7,8,9}; Lets rotate 3 times.
So We will be having 2 virital array array1 => {1.2.3} array2 => {4,5,6,7,8,9}
Now we will be reversing the virtual array1 -> {3,2,1} Now we will be reversing the virtual array2 -> {9,8,7,6,5,4}
Now the arrayOfNumber will be like => {3,2,1,9,8,7,6,5,4}
Now again we will be rotation the whole arrayOfNumber => {4,5,6,7,8,9,1,2,3}
Divide and Move
In this algorithm, we will be divinding the whole array into segments. To do this we will be first starting to find the GCD (Greatest Common Divisor) among the number of times we have to rotate and length of array.
Say No of Times we rotate is 3 Length of Array is 9
Then GCD is 3. Assumed our array is -> int[] arrayOfNumber = {1,2,3,4,5,6,7,8,9};
So we will have the segments each with 3 elements.
- Segment1 -> {1,2,3}
- Segment2 -> {4,5,6}
- Segment3 -> {7,8,9}
First we will be having the first element (initial index element -> 0) to swap in temporary argument. In our case its 1.
Then we will be move the element at 3rd index (0+3) to the initial Index (0). So now Array becomes like this
4 is moved {4,2,3,4,5,6,7,8,9};
Then we will be increment the position by 3 so we can move the next element. in case if its more than or equal to length of array, then we will subtract that value from length of array. Now the Array will look like below
7 is moved {4,2,3,7,5,6,7,8,9};
We will again will be increment the position to move the element, Now it will become 9, since its equal to length of array we will subtract it and now it becomes 0. If startIndex and new index to move element is equal we will break the while low. and at the end we will set the value of inital index element to old update position. So the array becomes like
1 is placed at end of while {4,2,3,7,5,6,1,8,9};
Now we will be increment the inital Index by 1. So now the temporary element will be at array[1] which is 2.
Now we will be elements will be replaced like this
- 2 <- 5
- 5 <- 8
- 8 <- 2
Now the updated the array will be like below. {4,5,3,7,8,6,1,2,9}
Next we will increment inital index by 1 so it becomes 2 now. and swap numbers left numbers
- 3 <- 6
- 6 <- 9
- 9 <- 3
Now the updated the array will be like below. {4,5,6,7,8,9,1,2,3}
private void rotateArray(int[] arr, int rotationTimes){
int numberOfItemsInSegment =findTheGCD(arr.length,rotationTimes);
for(int startIndex=0; startIndex<numberOfItemsInSegment;++startIndex){
int tempElement = arr[startIndex];
int indexToSwap = startIndex;
while (true) {
int nextIndexToswp = indexToSwap + rotationTimes;
if(nextIndexToswp>= arr.length){
nextIndexToswp = nextIndexToswp-arr.length;
}
if(startIndex==nextIndexToswp){
break;
}
int swapElement = arr[nextIndexToswp];
arr[indexToSwap] = swapElement;
indexToSwap=nextIndexToswp;
}
arr[indexToSwap] = tempElement;
}
// return arr;
}
private int findTheGCD(final int firstNumber, final int secondNumber){
if(secondNumber == 0){
return firstNumber;
}else{
return findTheGCD(secondNumber,firstNumber%secondNumber);
}
}